Towards a 3D Rotation Operator with a Quaternion Sandwich

All the nuts and bolts needed to go from quaternions to a quaternion rotation operator

Citation Note: I have borrowed this article’s content from Jack B. Kuipers’ seminal 1999 book on quaternions.

As an admirer of the book’s writing style, I submit that you are probably better off referring to Chapter 5 of the book. My motivation to write this regardless is twofold - to provide robotics practitioners with a one-stop-shop entry point to quaternions and challenge/improve my understanding of them. I claim no expertise in this topic but found it so fascinating that I decided to write about it.

Prerequisites: This is [2/3] article in my series on quaternions. For this article, I assume readers’ familiarity with basic quaternion algebra and rotation matrices and their basic properties.

Agenda

After going back and forth about it in my mind, I have decided to write about the quaternion rotation operator in two parts:

one that proposes a checklist of qualities necessary to be a reasonably good \(\mathbb{R}^3\) rotation operator and introduces the necessary tools to meet the checklist (this one)
one that discusses the geometric effects of the quaternion rotation operator (next one )

At the cost of clarity, I am probably risking losing readers’ attention and I only hope to keep you interested enough to stay aboard till the end of the series.

Quaternion Rotation Operator: Checklist

As we know, rotation matrices are \(3 \times 3\) orthogonal matrices with determinant 1 (unimodular). In fact, one can use any \(3 \times 3\) matrix \(R\) that satisfies the orthogonality and the unimodularityA matrix is unimodular if it has a determinant 1 or -1. But in this case, I am only talking about it being 1. properties to represent rotations in \(\mathbb{R}^3\). To find a vector \(\vec{v}\)’s rotated image \(\vec{w}\) under \(R\), we simply do the left matrix multiplication between \(R\) and a column matrix that whose entries are components of \(\vec{v}\) i.e., \(R\vec{v}\). It helps to recollect that the image \(\vec{w}\), thanks to the unimodularity of \(R\), has the same magnitude as \(\vec{v}\). If one were to invent a quaternion rotation operator, say \(R_{\mathbf{q}}\) (associated with the quaternion \(\mathbf{q}\)), it should satisfy the following:

\[\vec{w} = R_{\mathbf{q}}(\vec{v})\]

And more importantly, similar to rotation matrices, the operator \(R_{\mathbf{q}}\) should somehow bring about a notion of an axis and an angle of rotation to it. Of course the quaternion operator should also be able to reproduce other properties such as sequence of rotations i.e., have an equivalent form of \(R_1R_2R_3\vec{v}\), say \(R_{\mathbf{q}_1\mathbf{q}_2\mathbf{q}_3}\) and reverse rotations (e.g. \(R_1^{-1}R_2R_3\vec{v}\)) and more.

Perhaps we’ll worry about them later but at its core, it appears that the four fundamental desirable qualities of rotation operator \(R_{\mathbf{q}}\) are as follows:

\(R_{\mathbf{q}}\) should be able to operate on vectors.
\(R_{\mathbf{q}}\) should always output a vector in \(\mathbb{R}^3\).
\(R_{\mathbf{q}}\) shouldn’t scale the vectors.
\(R_{\mathbf{q}}\) should associate with an angleAlso an axis of rotation but we look at that in my next article. unique to \(\mathbf{q}\).

By the end of this article, we will see that this checklist is indeed fulfilled with quaternions albeit with some upgrades.

Pure Quaternions

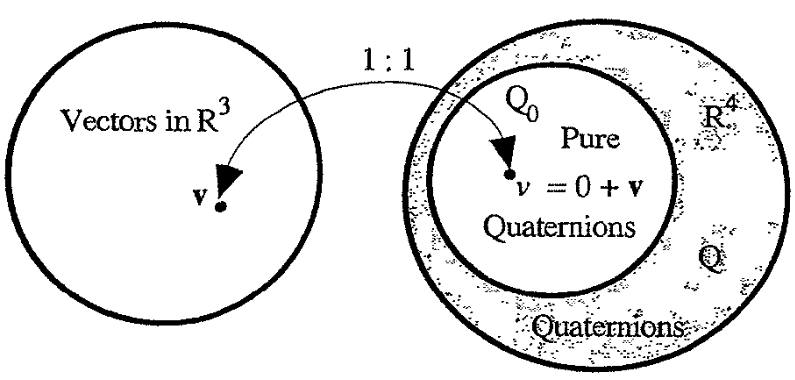
How can quaternions which are in \(\mathbb{R}^4\) operate on vectors in \(\mathbb{R}^3\)? Thanks to the Scalar + Vector model we discussed in , a vector can be interpreted as a pure quaternionOne might argue that real numbers are just scalar parts of quaternions. And why shouldn't they? i.e., \(\mathbf{v} = 0 + \vec{v}\). So \(Q_0\), the set of all pure quaternions, is a subset of \(Q\), the set of all quaternions. To that end, we can easily verify that:

Quaternion addition between any two pure quaternions
Quaternion multiplication between any two pure quaternions
Quaternion multiplication between a scalar and a pure quaternion

provide a one-to-one correspondence between \(\mathbb{R}^3\) and \(Q_0\). This is great and goes toward items 1 and 2 on our checklist.

Source: Jack B Kuipers. Quaternions and Rotation Sequences (1999)

However, multiplication (See Eq. \((1)\) from for clarity) between a general and a pure quaternion doesn’t always give us the same desirable one-to-one mapping. Still, it exists and is as follows:

\[\begin{aligned} \mathbf{q} \star \mathbf{v} &= (q_0 + \vec{q}) \star (0 + \vec{v}) \\ &= q_0 \cdot 0 - \vec{q} \cdot \vec{v} + 0 \cdot \vec{q} + q_0\vec{v} + \vec{q} \times \vec{v}\\ &= -\vec{q} \cdot \vec{v} + q_0\vec{v} + \vec{q} \times \vec{v} \hspace{10cm} \text{(1)} \end{aligned}\]

It is now clear that quaternion multiplication allows us to operate on vectors, as one should expect if one wants to define an \(\mathbb{R}^3\) rotation operator based on quaternions.

Item 1 in the list is checked. Quaternions can indeed operate on vectors, a.k.a pure quaternions, in a rather straightforward way.

Quaternion Sandwich Product

For quaternions to operate on vectors in \(\mathbb{R}^3\), it would have helped a lot in favour of item 2 in our list if their multiplication led to a one-to-one correspondence between \(\mathbb{R}^3\) and \(Q_0\). However, we see in Eq. \(\text{(1)}\) that the double product still has a scalar part. This is why the double products \(\mathbf{q} \star \mathbf{v}\) and \(\mathbf{v} \star \mathbf{q}\)The commutation does not change the scalar part. do not have a place in \(R_{\mathbf{q}}\). This suggests that the quaternion operator \(R_{\mathbf{q}}\) must have a triple or even higher order quaternion multiplication in it.

As one should, let us see if a triple product gives us what we want and what we want is to be able to stay in \(\mathbb{R}^3\) after the multiplication. Consider two general quaternions \(\mathbf{p}=p_0 + \vec{p}\) and \(\mathbf{q} = q_0 + \vec{q}\) and a pure quaternion \(\mathbf{v} = 0 + \vec{v}\). There are six possible products involving these three quaternions:

\[\begin{aligned} &\mathbf{p} \star \mathbf{q} \star \mathbf{v} \quad \mathbf{q} \star \mathbf{v} \star \mathbf{p} \quad \mathbf{v} \star \mathbf{p} \star \mathbf{q} \\ &\mathbf{q} \star \mathbf{p} \star \mathbf{v} \quad \mathbf{p} \star \mathbf{v} \star \mathbf{q} \quad \mathbf{v} \star \mathbf{q} \star \mathbf{p} \end{aligned}\]

On examination, we see that all products where \(\mathbf{p}\) and \(\mathbf{q}\) are together lead to the same problem we discussed earlier. Their product, regardless of the order, would return another general quaternion, making them double products. Our last hope seems to be in the two leftover triple products Although, I suspect the section's title must have given away the plot already.

\[\mathbf{p} \star \mathbf{v} \star \mathbf{q} \quad \quad \mathbf{q} \star \mathbf{v} \star \mathbf{p}\]

Despite the uninteresting exercise, lets expand the triple products, say \(\mathbf{p} \star \mathbf{v} \star \mathbf{q}\).

\[\begin{aligned} \mathbf{p} \star \mathbf{v} \star \mathbf{q} &= (\mathbf{p} \star \mathbf{v}) \star \mathbf{q} \\ &= (-\vec{p}\cdot\vec{v} + p_0\vec{v} + \vec{p} \times \vec{v}) \star \mathbf{q} \\ &= - q_0 \vec{p}\cdot\vec{v} - (p_0\vec{v} + \vec{p} \times \vec{v}) \cdot \vec{q} + (-\vec{p}\cdot\vec{v})\cdot\vec{q} \\ &\quad + q_0(p_0\vec{v} + \vec{p} \times \vec{v}) + (p_0\vec{v} + \vec{p} \times \vec{v}) \times \vec{q} \\ &= - q_0 (\vec{p}\cdot\vec{v}) - p_0(\vec{v} \cdot \vec{q}) - (\vec{p} \times \vec{v}) \cdot \vec{q} \\ & \quad - (\vec{p}\cdot\vec{v})\cdot\vec{q} + q_0(p_0\vec{v} + \vec{p} \times \vec{v}) \\ & \quad + (p_0\vec{v} + \vec{p} \times \vec{v}) \times \vec{q} \end{aligned}\]

Separating out the scalar part from above, we have:

\[- q_0 (\vec{p}\cdot\vec{v}) - p_0(\vec{v} \cdot \vec{q}) - (\vec{p} \times \vec{v}) \cdot \vec{q}\]

We may rewrite this with a little bit of vector algebra trickery as:

\[- q_0 (\vec{p}\cdot\vec{v}) - p_0(\vec{v} \cdot \vec{q}) + (\vec{p} \times \vec{q}) \cdot \vec{v}\]

Recall that if this triple product were to be inside \(R_{\mathbf{q}}\), it should output a pure quaternion. So we have to choose \(\mathbf{p}\) and \(\mathbf{q}\) such that the scalar part goes to \(0\) for all pure quaternions. Examining the cross product term, we see that \((\vec{p} \times \vec{q}) \cdot \vec{v}\) would go to \(0\) if \(\mathbf{p}\) and \(\mathbf{q}\) are parallel to each other i.e., if \(\mathbf{p} = k\mathbf{q}\) for non-zero \(k\) since we are dealing with non-zero vectors \(\vec{p}\) and \(\vec{q}\)Note that this is a fair assumption to make. We have full control over the quaternions; however, there is not much on the vector to be rotated.. Substituting this back in the scalar part expression, we get

\[\begin{aligned} &\Rightarrow - q_0 (k\vec{q}\cdot\vec{v}) - p_0(\vec{v} \cdot \vec{q}) + (k\vec{q} \times \vec{q}) \cdot \vec{v} \\ &\Rightarrow - q_0k (\vec{q}\cdot\vec{v}) - p_0(\vec{q}\cdot\vec{v}) + 0 \cdot \vec{v} \\ &\Rightarrow -(q_0k+p_0)(\vec{q}\cdot\vec{v}) \end{aligned}\]

It is easy to verify that the above expression goes to \(0\) when \(\vec{q}\) and \(\vec{v}\) are parallel to each other or if \(k=-1\) and \(p_0 = q_0\) which would simply mean that

\[\mathbf{p} = p_0 + \vec{p} = q_0 -\vec{q} \Rightarrow \mathbf{p} = \mathbf{q}^{\ast}\]

From this discussion, we obtain two triple quaternion products that always output a pure quaternion whenever they sandwich (hence the name) a pure quaternion, although it is not yet clear how they differ from each other

\[\mathbf{q} \star \mathbf{v} \star \mathbf{q}^{\ast} \quad \quad \mathbf{q}^{\ast} \star \mathbf{v} \star \mathbf{q}\]

The algebraic action of \(\mathbf{w} = \mathbf{q} \star \mathbf{v} \star \mathbf{q}^{\ast}\) is illustrated in the figure below.

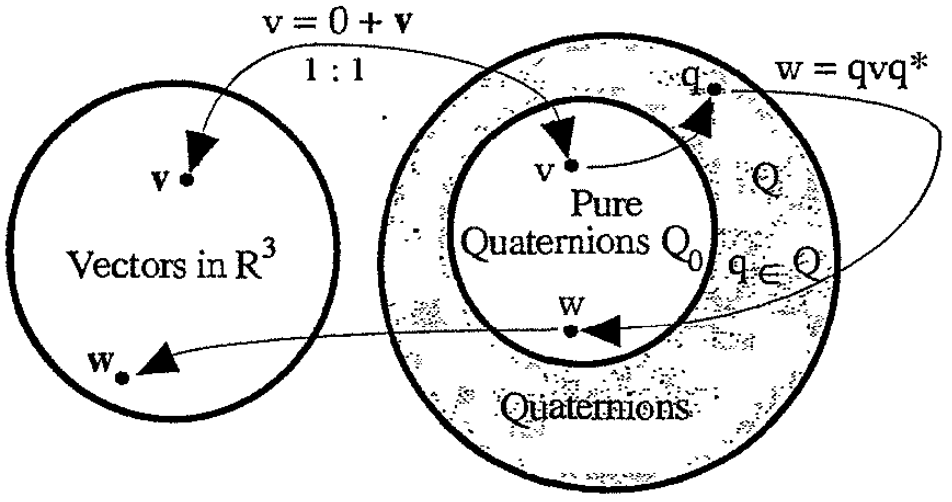
A natural question to raise is - what geometric interpretation can we give this sandwich product? I study their geometric considerations more closely in my next article . But to see the geometrics, it helps to associate an angle with a quaternion. Is there some way to do that, analogous to the rotation matrices? In the later parts of this article, you will see that there is indeed a way to associate an angle with quaternions.

Item 2 in the list is checked as long as \(R_{\mathbf{q}}\) has sandwich product.

Unit Quaternions

Unit quaternions i.e., \(\Vert \mathbf{q} \Vert^2 = (\mathbf{q}^{\ast} \star \mathbf{q}) = (\mathbf{q} \star \mathbf{q}^{\ast}) = 1\) are simply quaternions whose norm is 1. What is worth noting about unit quaternions is that their quaternion multiplication preserves membership in the \(\mathbf{S}^3\) spaceA sphere in 4-dimensional space where each point represents a quaternion with magnitude 1. of unit quaternions. That is, the quaternion product of two unit quaternions \(\mathbf{p}\) and \(\mathbf{q}\) i.e., \(\mathbf{p} \star \mathbf{q}\) will also be a unit quaternion and hence will still belong to the unit-sphere in \(\mathbf{S}^3\). This convenient geometric property allows us to do many cool things such as non-Euclidean calculus with quaternions, something that could be exploited to learn geometry-aware models, say, a dynamical system on robot’s trajectory of both positions and orientations. More importantly to our journey, it should be clear that the rotation operator \(R_{\mathbf{q}}\) should include unit quaternions and not general quaternions.

Perhaps this is already obvious (from Eq. \((4)\) and Eq. \((5)\) of ), the quaternion sandwich product with unit quaternions wouldn’t change the magnitude of the pure quaternion \(\mathbf{v}\).

\[\begin{aligned} \Vert \mathbf{q} \star \mathbf{v} \star \mathbf{q}^{\ast} \Vert^2 &= \Vert \mathbf{q} \Vert^2 \Vert \mathbf{v} \Vert^2 \Vert \mathbf{q}^{\ast} \Vert^2 \\ &= \Vert \mathbf{v} \Vert^2 \end{aligned}\]

In fact, even for higher-order multiplication with unit quaternions, we see that the norm of the factors is preserved. Say, we have \(n\) unit quaternions \(\{\mathbf{q}_1, \mathbf{q}_2, ..., \mathbf{q}_n\}\) and a general quaternion \(\mathbf{p}\). The squared norm of their products in any order yields the same, as follows:

\[\begin{aligned} \Vert \mathbf{q}_1 \star ... \star \mathbf{p} \star ... \star \mathbf{q}_n \Vert^2 &= \Vert \mathbf{p} \star \mathbf{q}_1 \star ... \star \mathbf{q}_n \Vert^2 \\ &= \Vert \mathbf{q}_1 \star ... \star \mathbf{q}_n \star \mathbf{p} \Vert^2 \\ &= \Vert \mathbf{p} \Vert^2 \end{aligned}\]

Item 3 in the list is checked as long as the \(\mathbf{q}\) in \(R_{\mathbf{q}}\) is a unit quaternion.

Polar Form

(Optional) Complex Numbers

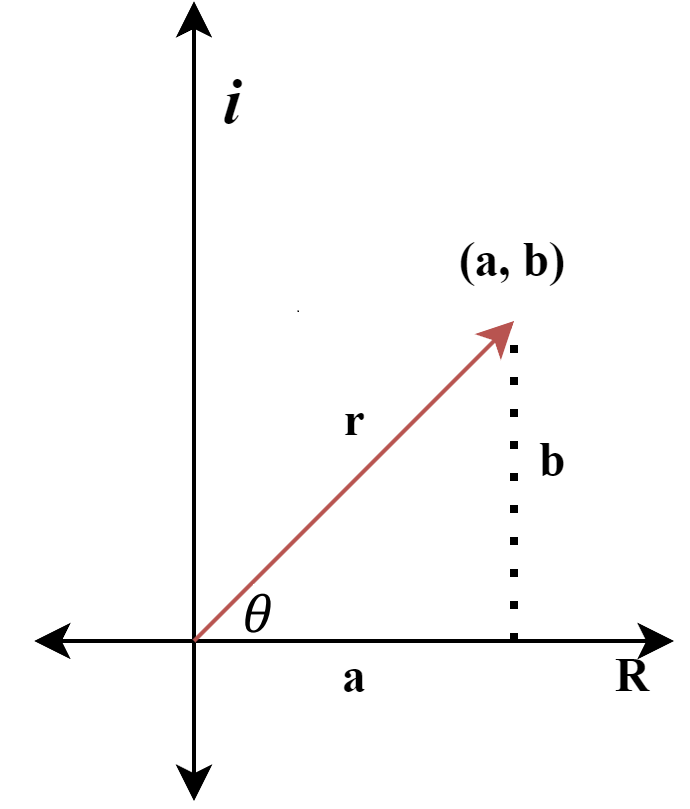
Complex numbersI bring complex numbers into the discussion for familiarity and easy visualisations. If this is obvious to you, please skip to the next subsection. have an intuitive alternate form of representation to them. A complex number \(z = a + ib\) can be interpreted as a 2D vector on a complex plane where the horizontal axis is the real axis and the vertical axis is the imaginary axis, as shown in the figure below. A natural consequence of this is the polar or trigonometric form where \(z = a + ib\) can be represented with its polar pair \((r, \theta)\) such that \(r = \sqrt{a^2 + b^2}\) (norm) and \(\theta = \arctan (\frac{b}{a})\) (angle between complex vector and the real axes), from this it follows that \(\cos \theta = \frac{a}{r}\) and \(\sin \theta = \frac{b}{r}\).

Now, we see that the following holds:

\[\begin{aligned} z &= a + ib \\ &= r \cos \theta + i (r \sin \theta) \\ &= r (\cos \theta + i \sin \theta) \end{aligned}\]

Consequently, one can obtain the complex conjugate by simply replacing \(\theta\) with \(-\theta\), i.e.,

\[\begin{aligned} z^{\ast} &= r (\cos (-\theta) + i \sin (-\theta)) \\ &= r(\cos \theta - i \sin \theta) \end{aligned}\]

It helps to know that one can extend this to quaternions and write them in polar form just as well.

(Optional) A Special Property of Complex Product

The complex polar form allows us to spot a special property inherent to complex numbers. Consider two complex numbers:

\[\begin{aligned} z_1 &= r_1(\cos \theta_1 + i \sin \theta_1)\\ z_2 &= r_2(\cos \theta_2 + i \sin \theta_2) \end{aligned}\]

Their complex multiplication is as follows:

\[\begin{aligned} z_1z_2 &= r_1(\cos \theta_1 + i \sin \theta_1) . r_2(\cos \theta_2 + i \sin \theta_2) \\ &= r_1r_2(\cos \theta_1 \cos \theta_2 + i \cos \theta_1 \sin \theta_2 + i \sin \theta_1 \cos \theta_2 \\ & \quad - \sin \theta_1 \sin \theta_2) \\ &= r_1r_2(\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \\ &\quad + i (\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2)) \\ &= r_1r_2(\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)) \end{aligned}\]

The geometric interpretation of the complex product is clear now. When two complex numbers are multiplied, you notice that the output complex number has an associated angle that is exactly the sum of angles associated with the multiplicands and has a magnitude equal to the product of magnitudes of the multiplicands.

This is true if a3+ib3 = (a1+ib1)(a2+ib2)

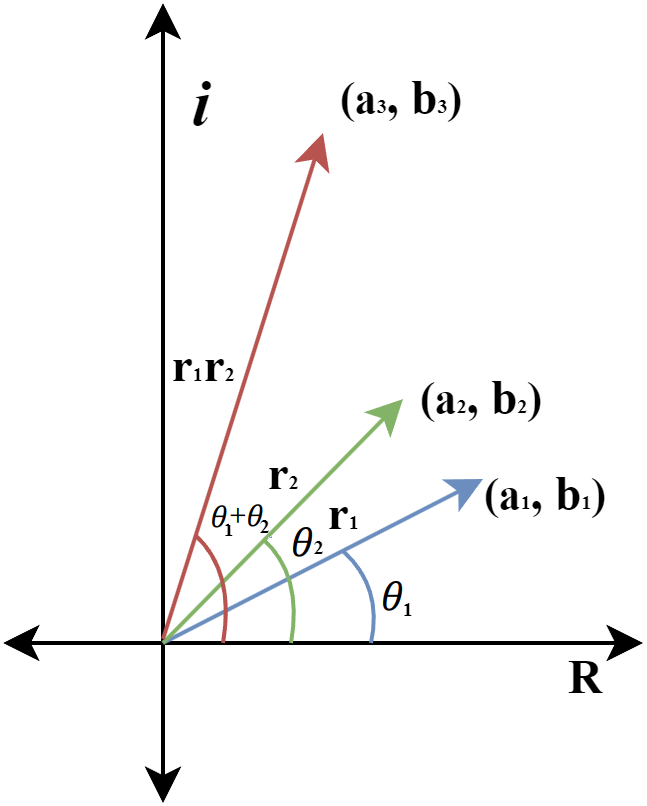
We can also verify that multiplying a complex number with another complex number’s conjugate essentially subtracts or cancels the former’s angle by latter’s angle. All of this is quite suggestive that complex numbers can be used to represent 2D rotations (also scaling for non-unit complex numbers), which is perhaps obvious or well-known to many. However, does this extend to quaternions? Yes. No. Maybe. We hope to find out soon!

Quaternions

Quaternions, particularly unit quaternions, can also be written in polar form, albeit the interpretation of the angle \(\theta\) may not be as straightforward as it is for complex numbers. We know that a unit quaternion \(\mathbf{q} = q_0 + \vec{q}\) has norm 1 i.e., \(q_0^2 + \Vert \vec{q} \Vert^2 = 1\). And that for any angle \(\theta\), we know that \(\cos^2 \theta + \sin^2 \theta = 1\) holds. So there must be an angle \(\theta\) such that

\[\begin{aligned} \cos^2 \theta &= q_0^2 \\ \sin^2 \theta &= \Vert \vec{q} \Vert^2 \end{aligned}\]

The angle \(\theta\) can be defined uniquely as long as it stays within \((-\pi, \pi]\). But this is it, we now have an angle (although still unclear what it represents) associated with the quaternion \(\mathbf{q}\). We can take this form further by defining a unit vector \(\vec{u}\), which represents the direction of \(\vec{q}\):

\[\vec{u} = \frac{\vec{q}}{\Vert \vec{q} \Vert} = \frac{\vec{q}}{\sin \theta}\]

Then, we may be able to write all unit quaternions in terms of the associated angle \(\theta\) and the unit vector \(\vec{u}\) as

\[\mathbf{q} = q_0 + \vec{q} = \cos \theta + \vec{u} \sin \theta\]

Note, similar to complex numbers, for a quaternion expressed in this form, substituting \(-\theta\) for \(\theta\) (whatever geometric meaning the angle \(\theta\) might have) we get the complex conjugate of \(\mathbf{q}\). Which is,

\[\begin{aligned} \mathbf{q}^{\ast} &= \cos (-\theta) + \vec{u} \sin (-\theta) \\ &= \cos \theta - \vec{u} \sin \theta \end{aligned}\]

It is not too difficult to verify that if we replace \(\theta\) by \(-\theta\) of \(\mathbf{q}\) in one sandwich product, we get the other one out. So by the appropriate choice of the angle \(\theta\) these operators may, in fact, represent the same geometric transformation. I discuss more of this in

A Special Property of Quaternion Product

I hope you will have figured out where I am going with this by now. Consider two unit quaternions:

\[\begin{aligned} \mathbf{q}_1 &= \cos \theta_1 + \vec{u} \sin \theta_1\\ \mathbf{q}_2 &= \cos \theta_2 + \vec{u} \sin \theta_2 \end{aligned}\]

The quaternion product of these two (see \((1)\) in for clarity) gives

\[\begin{aligned} \mathbf{q}_1 \star \mathbf{q}_2 &= (\cos \theta_1 + \vec{u} \sin \theta_1)(\cos \theta_2 + \vec{u} \sin \theta_2) \\ &= \cos \theta_1 \cos \theta_2 - (\vec{u} \sin \theta_1) \cdot (\vec{u} \sin \theta_2) \\ & \quad + \cos \theta_1 (\vec{u} \sin \theta_2) + \cos \theta_2 (\vec{u} \sin \theta_1) + \vec{u} \sin \theta_1 \times \vec{u} \sin \theta_2 \\ &= \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \\ & \quad + \vec{u} (\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2)\\ &= \cos (\theta_1 + \theta_2) + \vec{u} \sin (\theta_1 + \theta_2) \end{aligned}\]

Once again, very similar to complex numbers, this is an interesting result and has an important geometric implication. It says if we multiply two unit quaternions \(\mathbf{q}_1\) and \(\mathbf{q}_2\), each having the same unit vector \(\vec{u}\) in them, then the product is also a unit quaternion having this same unit vector \(\vec{u}\). And, associated with it is an angle that is exactly the sum of angles associated with \(\mathbf{q}_1\) and \(\mathbf{q}_2\). If, in fact, the quaternion rotation operator represents rotation, this property suggests that there is a possibility of sequencing rotations with different \(\mathbf{q}\)s, a property enjoyed by the rotation matrices.

Item 4 in the list is checked as we showed that it is possible to associate an angle \(\theta\) with unit quaternions.

Conclusion

We looked at some quaternion tricks, upgrades and forms that allow us to go from a 4-tuple vector with seemingly arbitrary product rules to a 3D rotation operator. We defined a checklist at the beginning and I would like to think that I convinced you that quaternions indeed meet all of them without room for doubtI would love to answer or just ponder your questions, if any. Please feel free to write them in the comments below.. Given a 3D vector as a pure quaternion \(\mathbf{v}\) and a unit quaternion \(\mathbf{q}\), we have seen considerable evidence that the quaternion rotation operator \(R_{\mathbf{q}}\) should have the form

\[R_{\mathbf{q}}(\mathbf{v}) = \mathbf{q} \star \mathbf{v} \star \mathbf{q}^{\ast} \quad \text{or} \quad \mathbf{q}^{\ast} \star \mathbf{v} \star \mathbf{q}\]

and that it is in some way related to rotations in \(\mathbb{R}^3\). However, I accept that there is still a lot to be discussed and investigated, especially the geometric effects of the sandwich product when applied to an arbitrary \(\mathbb{R}^3\) vector. I wrote about exactly this in the next article of this series . There we take the sandwich product to a couple of field tests and reverse engineer the output vector with some convenient visualisations.