Quaternion Rotation Operator

Exploring the geometric effects of the quaternion rotation operator

Citation Note: I have borrowed this article’s content from Jack B. Kuipers’ seminal 1999 book on quaternions.

As an admirer of the book’s writing style, I submit that you are probably better off referring to Chapter 5 of the book. My motivation to write this regardless is twofold - to provide robotics practitioners with a one-stop-shop entry point to quaternions and challenge/improve my understanding of them. I claim no expertise in this topic but found it so fascinating that I decided to write about it.

Prerequisites: This is [3/3] article in my series on quaternions. For this article, I assume readers’ familiarity with basic quaternion algebra and some quaternion variants I discussed in .

Earlier, we saw a great deal of evidence that quaternions indeed can represent \(\mathbb{R}^3\) rotations. With the checked list in mind, we can now safely define the quaternion rotation operator and apply some tests to understand its geometric effects on \(\mathbb{R}^3\) vectors. All quaternions you see in this article are to be assumed units.

Quaternion Rotation Operator: Definition

Let \(\mathbf{q}\) be a unit quaternion, and \(\vec{v}\) be a vector in \(\mathbb{R}^3\) (pure quaternion); we define two rotation operators as follows:

\[\begin{aligned} R_{\mathbf{q}}(\vec{v}) &= \mathbf{q} \star \vec{v} \star \mathbf{q}^{\ast} \\ R_{\mathbf{q}^{\ast}}(\vec{v}) &= \mathbf{q}^{\ast} \star \vec{v} \star \mathbf{q} \end{aligned}\]

For comparison, writing out the operator algorithm will be helpful.

\[\begin{aligned} R_{\mathbf{q}}(\vec{v}) &= \mathbf{q} \star \vec{v} \star \mathbf{q}^{\ast} \\ &= (2q_0^2-1)\vec{v} + 2(\vec{q}\cdot \vec{v})\vec{q} + 2q_0(\vec{q} \times \vec{v}) \\ R_{\mathbf{q}^{\ast}}(\vec{v}) &= \mathbf{q}^{\ast} \star \vec{v} \star \mathbf{q} \\ &= (q_0^2-\Vert \vec{q} \Vert^2)\vec{v} + 2(\vec{q}\cdot \vec{v})\vec{q} + 2q_0(\vec{q} \times \vec{v}) \end{aligned}\]

Without formal proof, I claim that these operators indeed rotate \(\vec{v}\) in \(\mathbb{R}^3\). Through some carefully designed tests, I hope to convince you on the same by answering the following key questions about \(R_{\mathbf{q}}\):

Let us start by reverse engineering the output of \(R_{\mathbf{q}}(\mathbf{v})\) to answer the questions.

Incremental Test

For this test, let us make our lives easy and work with simple quaternions and simple vectors that are easy to visualise in our heads. Suppose that the unit quaternion \(\mathbf{q}\) in \(R_{\mathbf{q}}(\vec{v})\) has a basis vector

\[\vec{u} = 0i + 0j + 1k = k \quad (\text{or }\left[\begin{matrix} 0 \\ 0 \\ 1\end{matrix}\right])\]

where \(\{i, j, k\}\) are the standard basis vectors in \(\mathbb{R}^3\), that define the coordinate frame. Let us now look at \(\mathbf{q}\) in polar form (recall section Polar Form from ):

\[\mathbf{q} = \cos \theta + k \sin \theta\]

Assume that the associated angle \(\theta\) is a very small positive angle. This assumption is helpful when comparing the input vector with the operator’s output vector. We want to verify if \(R_{\mathbf{q}}(\vec{v})\) merely “tweaks” the input vector when the associated angle is a very small positive value. Conveniently, for very small positive angles, we can round things up nicely, i.e., \(\cos \theta \approx 1\) and \(\sin \theta \approx \theta\) so the quaternion \(\mathbf{q}\) may be re-written as

\[\mathbf{q} \approx 1 + k\theta\]

In the spirit of simplicity, suppose that you want to rotate another basis vector \(\vec{v} = 1i + 0j + 0k = i\) (or \(\left[\begin{matrix} 1 \\ 0 \\ 0\end{matrix}\right]\)). Let us see what the operator \(R_{\mathbf{q}}(\vec{v})\) outputs for this carefully chosen \(\mathbf{q}\) and \(\vec{v}\):

\[\begin{aligned} \vec{w} &= R_{\mathbf{q}}(\vec{v}) = \mathbf{q} \star i \star \mathbf{q}^{\ast} \\ &= (1+k\theta)(i)(1-k\theta) \\ &= (1+k\theta)(i+j\theta) \\ \vec{w} &= i + 2\theta j \quad (\text{or }\left[\begin{matrix} 1 \\ 2\theta \\ 0\end{matrix}\right]) \end{aligned}\]

We can interpret this result to mean that the input vector \(i\) has been “tweaked” by some angle to produce the output vector \(i + 2\theta j\). Firstly, for completeness, let us examine the length of \(\vec{w}\)

\[\Vert \vec{w} \Vert = \sqrt{(1)^2 + (2\theta)^2} \approx 1 \quad (\text{Since }\theta \approx 0)\]

The length of the \(\vec{w}\) is still \(1\) (well almost, if you ignore the very small value \(\theta^2\))Note that we have no restriction on the length of the vector to be rotated, just that the output vector's length _should not_ change after rotation and it does not so this is good news. . Now, lets think about the angle between rotated image \(\vec{w}\) and \(\vec{v}\). It helps to mentally visualize this rotation as a vector that was earlier pointing at \(i\) (or \(\left[\begin{matrix} 1 \\ 0 \\ 0\end{matrix}\right]\)) and is now pointing at \(i+2\theta j\) (or \(\left[\begin{matrix} 1 \\ 2\theta \\ 0\end{matrix}\right]\)). Geometrically, it so appears that \(i\) is rotated counter-clockwise about the axis \(k\) by \(2\theta\) angle. Let us verify this by checking the angle of rotation \(\alpha\) between \(\vec{w}\) and \(\vec{v}\), which can be given by:

\[\begin{aligned} \tan \alpha &= \frac{\Vert w \times v \Vert}{(w \cdot v)} \\ &= \frac{\Vert i + 2\theta j \times i \Vert}{(i+2\theta j) \cdot (i)} \\ &= \frac{\Vert 2\theta k \Vert}{(1 \cdot 1 + 2\theta \cdot 0 + 0 \cdot 0)}\\ &= \frac{2\theta}{1} \quad (\text{Geometrically, just } \frac{\text{opposite}}{\text{adjacent}})\\ \alpha &\approx 2\theta \quad (\text{Since } \tan \alpha \approx \alpha \text{ when } \alpha \approx 0^+) \\ \alpha &\approx\text{A very small positive angle} \end{aligned}\]

which seems fair for the choice of a very small positive angle \(\theta\). Despite some (potentially uneasy) approximations, we now have a pretty good idea of the direction, axis and angle of rotation associated with \(R_{\mathbf{q}}\). The general rule goes as follows:

Given a unit quaternion \(\mathbf{q} = \cos \theta + \vec{u} \sin \theta\) and a vector \(\vec{v}\) in \(\mathbb{R}^3\), \(R_{\mathbf{q}}(\vec{v})\) rotates \(\vec{v}\) in counter-clockwise direction about the axis of \(\vec{u}\) by angle \(2\theta\).

See the figure above for clarity. We can further verify this visually (at least the axis and direction of rotation) for varying \(\theta\) values in Ben Eater’s interactive quaternion visualisation, see the following animation.

The visualisation shows rotation from the above example but with varying associated angle.

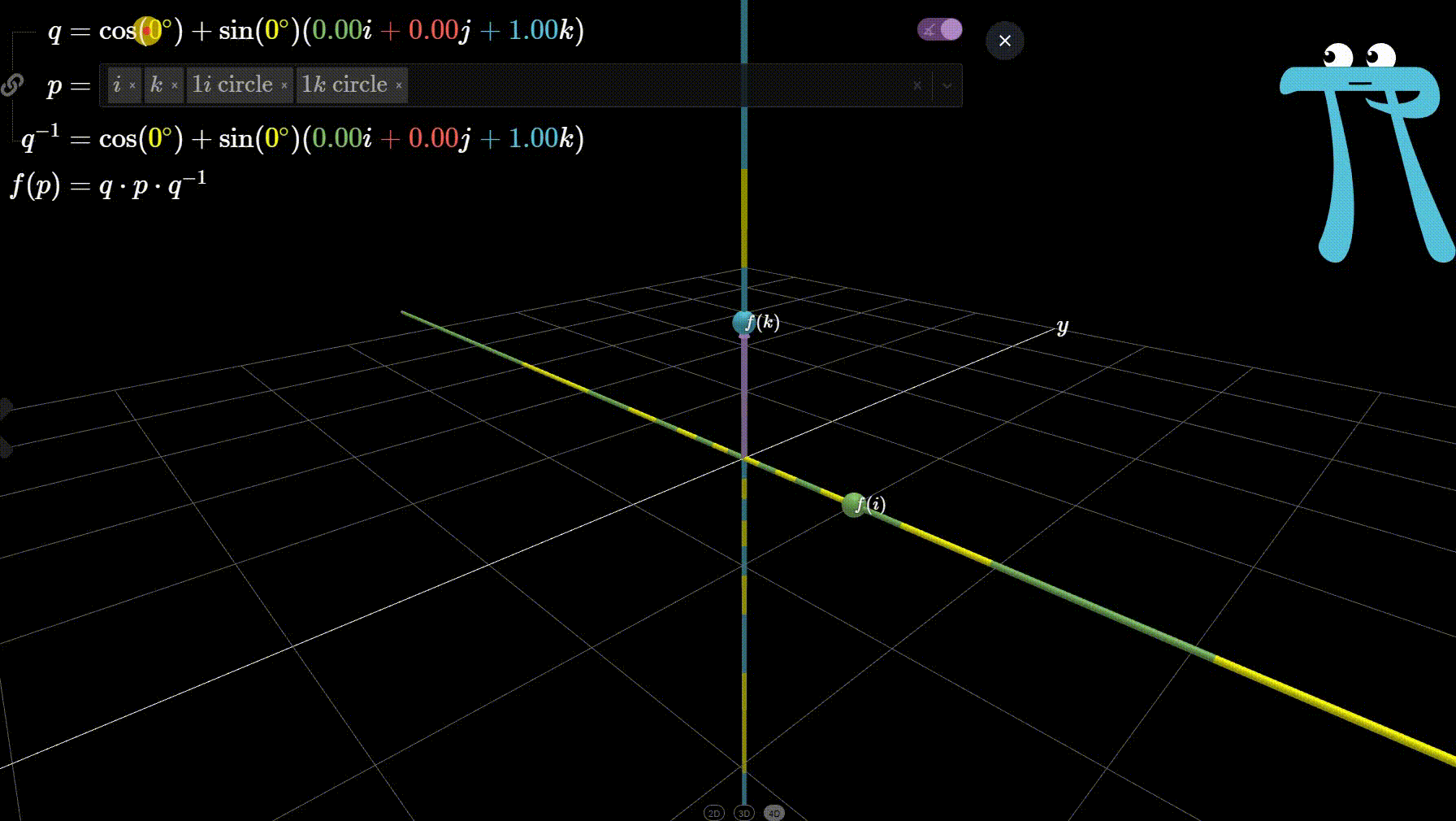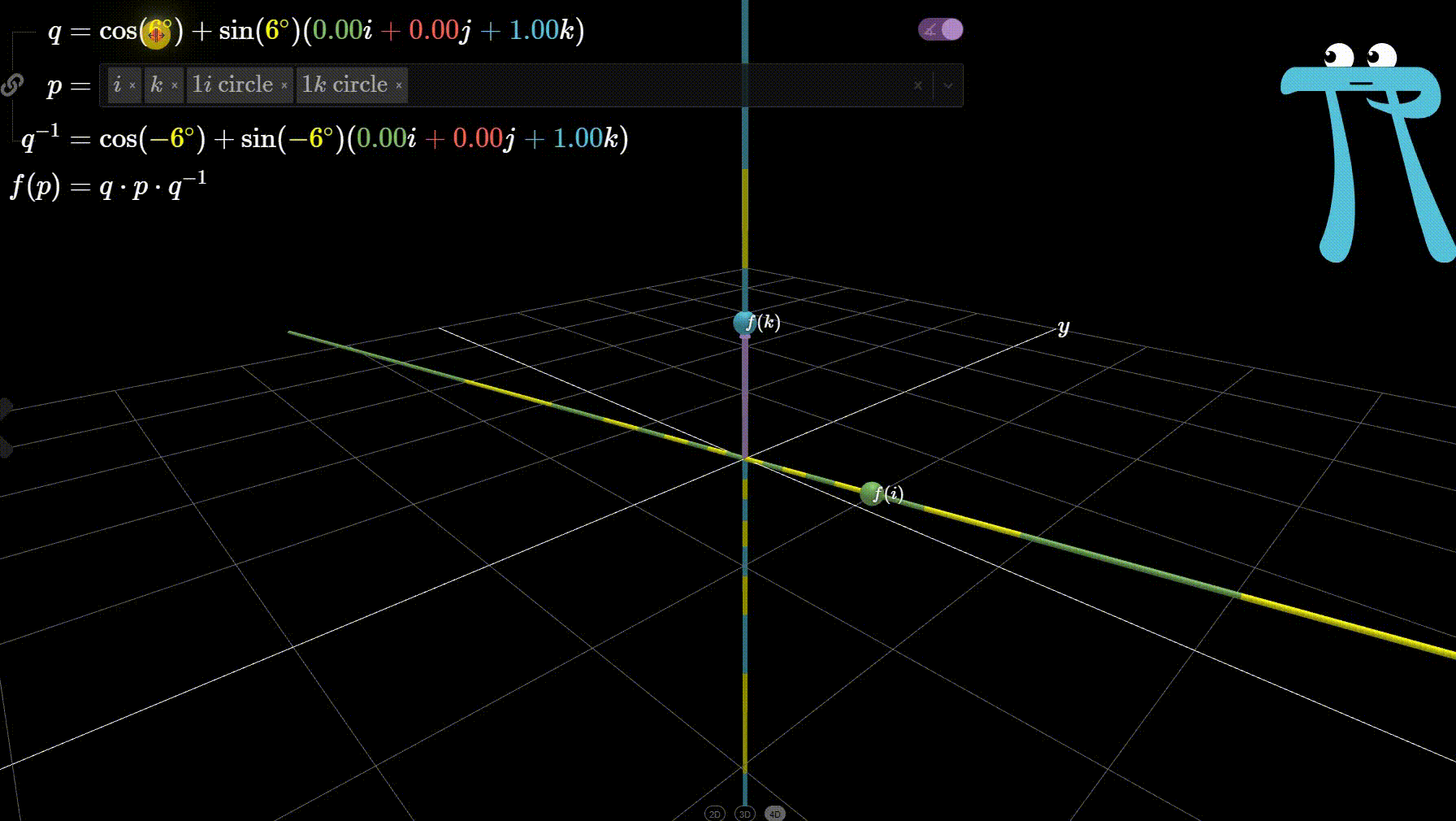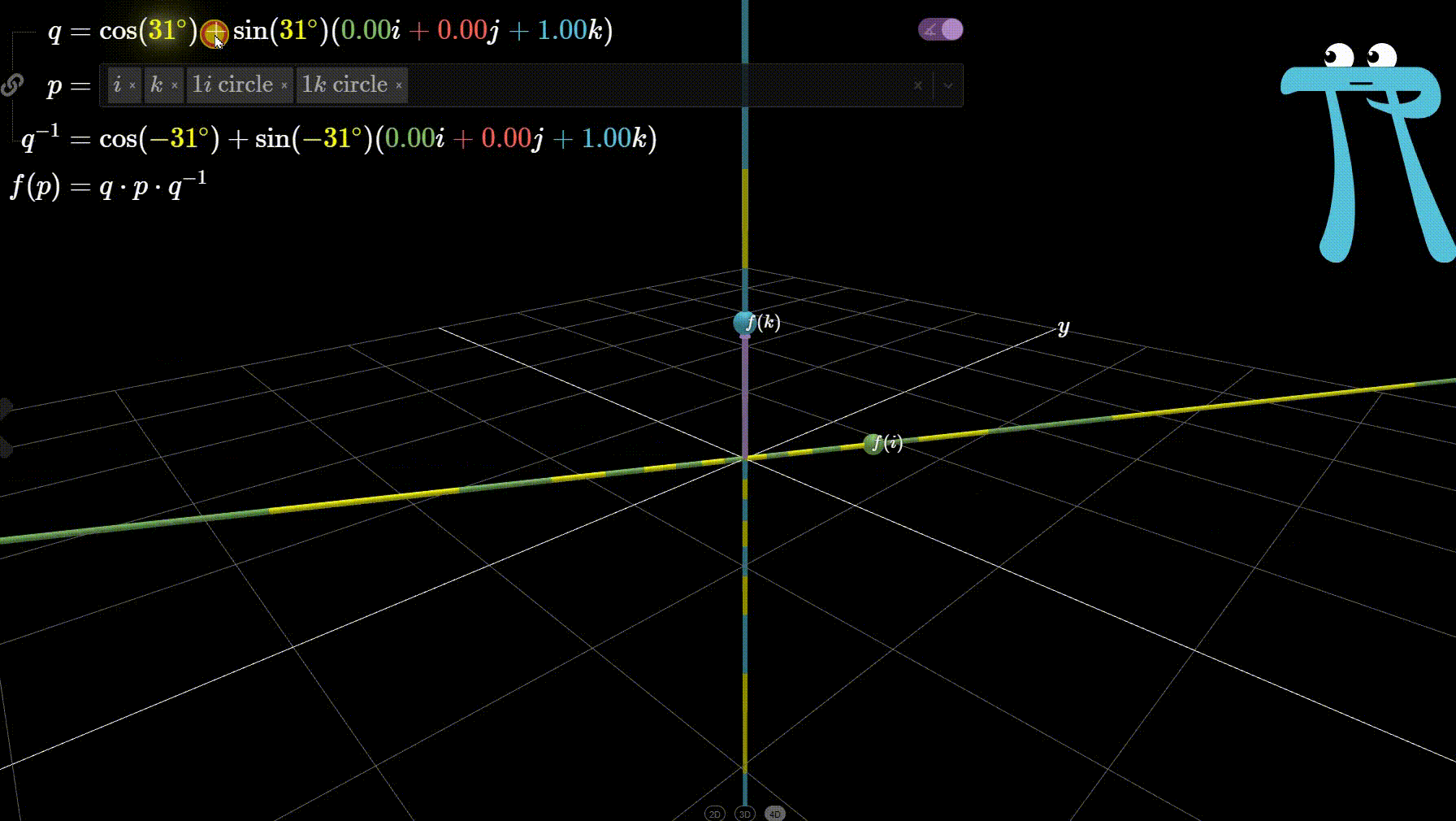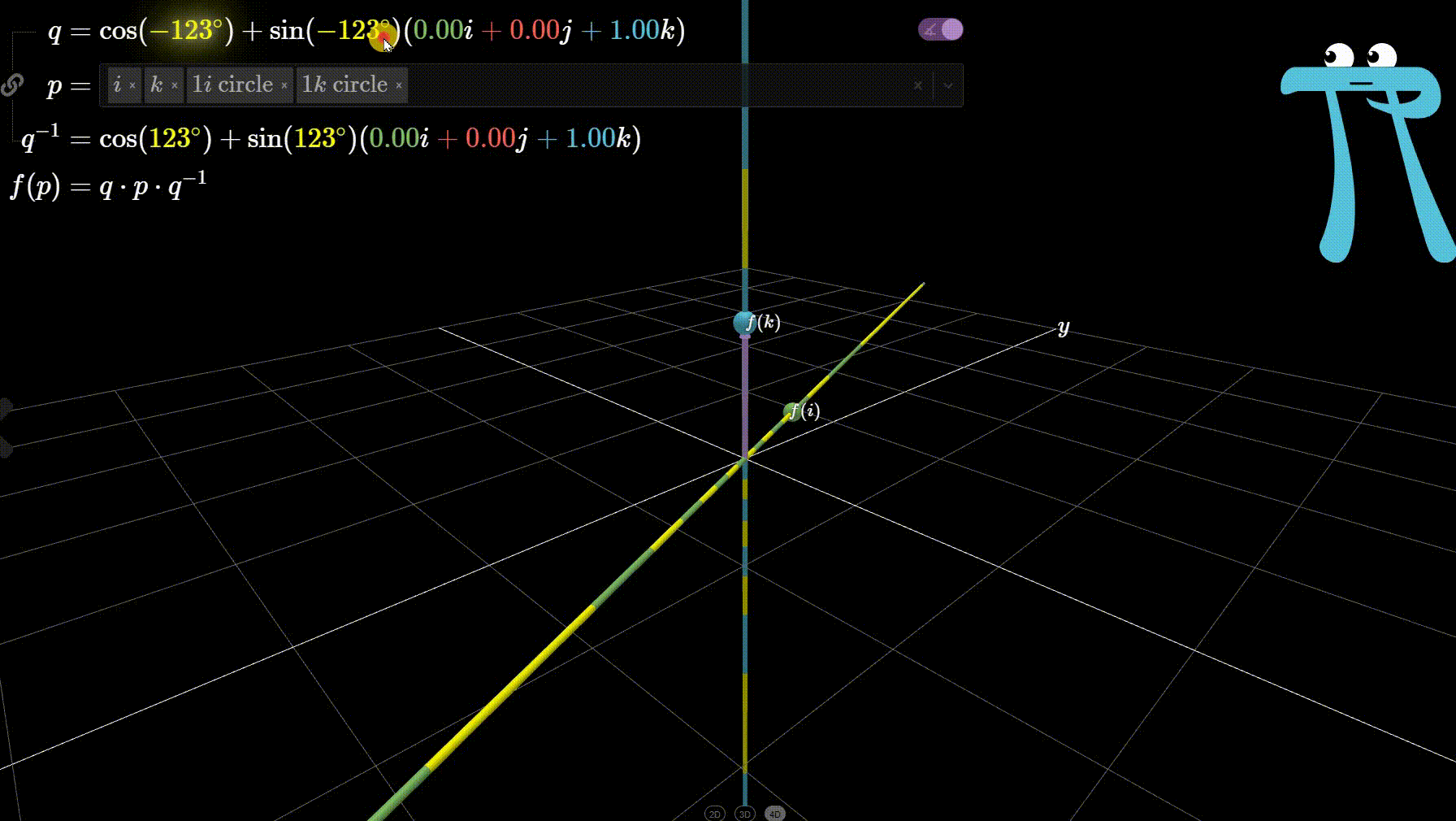
I encourage you to verify other rotations, say when \(\vec{u} = i\) or \(j\). If you did verify, for the case \(\vec{u} = i\), you will have seen no rotation at all. This implies, perhaps obviously, that any vector \(\vec{v}\) which lies on the axis of rotation \(\vec{u}\) must be invariant under \(R_{\mathbf{q}}(\vec{v})\).

Angle Test

When I first saw the incremental test, I was left uneasy and sceptical of the angle of rotation due to the approximations made. But we can be sure of the claims made on the angle of rotation with a simple angle test. Let us choose a unit quaternion with the associated angle \(\theta=\frac{\pi}{6}\) while keeping the axis of rotation \(\vec{u}\) as the same basis vector \(k\). Then we have the following quaternion

\[\begin{aligned} \mathbf{q} = \cos \theta + k \sin \theta &= \cos (\frac{\pi}{6}) + k \sin (\frac{\pi}{6}) \\ &= \frac{\sqrt{3}}{2} + \frac{1}{2} k \end{aligned}\]

Let us apply the operator \(R_{\mathbf{q}}(\vec{v})\) on the same basis vector \(\vec{v} = 1i + 0j + 0k = i\). We have

\[\begin{aligned} \vec{w} &= R_{\mathbf{q}}(\vec{v}) = (\frac{\sqrt{3}}{2} + \frac{1}{2} k)(i)(\frac{\sqrt{3}}{2} - \frac{1}{2} k) \\ &= (\frac{\sqrt{3}}{2} i + \frac{1}{2} j)(\frac{\sqrt{3}}{2} - \frac{1}{2} k) \\ &= \frac{3}{4} i + \frac{\sqrt{3}}{4} j + \frac{\sqrt{3}}{4} j - \frac{1}{4} i \\ &= \frac{1}{2} i + \frac{\sqrt{3}}{2} j \end{aligned}\]

As seen earlier, the angle between \(\frac{1}{2} i + \frac{\sqrt{3}}{2} j\) and \(i\) is given by

\[\begin{aligned} \tan \alpha &= \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} \quad (\frac{\text{opposite}}{\text{adjacent}}) \\ &= \sqrt{3} \\ \alpha &= \arctan \sqrt{3} \\ \alpha &= \frac{\pi}{3} \quad (= 2\theta) \end{aligned}\]

We can now confirm that the angle of rotation for a unit quaternion \(\mathbf{q}\) with an associated angle \(\theta\) is indeed \(2\theta\). Always choose a quaternion that has an associate angle half that of your target rotation angle.

Rotation Perspective

At this point, we have everything we need to geometrically compare \(R_{\mathbf{q}}(\vec{v})\) and \(R_{\mathbf{q}^{\ast}}(\vec{v})\). Consider the example from the Angle Test, there are two possible interpretations of \(\vec{w}\). One is that \(\vec{v}\) has rotated about \(k\)-axis by \(+\frac{\pi}{3}\) angle that is in a counter-clockwise direction with a fixed coordinate frame \(\{i, j, k\}\), this is called point rotation. Another one is that the coordinate frame \(\{i, j, k\}\) has rotated about \(k\)-axis by \(-\frac{\pi}{3}\) angle that is in clockwise direction with a fixed vector \(\vec{v}\), this is called frame rotation. Which of these two perspectives is to be preferred in a given application is usually a subjective matter - a decision made by the practitioner. This is precisely where the conjugate rotation operator \(R_{\mathbf{q}^{\ast}}(\vec{v})\) comes into play.

One can easily verify for the example in the Incremental Test, where \(\mathbf{q} \approx 1 + k\theta\) and \(\vec{v} = 1i + 0j + 0k = i\), applying the conjugate rotation operator \(R_{\mathbf{q}^{\ast}}(\vec{v})\) on \(\vec{v}\) would yield the following:

\[\vec{w}^{\ast} = R_{\mathbf{q}^{\ast}}(\vec{v}) = 1 - 2\theta j\]

Comparing this with the \(\vec{w} = 1 + 2\theta j\) suggests that the difference between \(R_{\mathbf{q}}(\vec{v})\) and \(R_{\mathbf{q}^{\ast}}(\vec{v})\) is simply the direction of rotation. One must be careful here, however, as seen in section Polar Form of , \(\theta\) has to restrict to the domain \((-\pi, \pi]\). So \(\theta\) can be both negative and positive, which makes it very difficult to differentiate between these two operators. Basically, \(R_{\mathbf{q}}(\vec{v})\) can do what \(R_{\mathbf{q}^{\ast}}(\vec{v})\) does with an appropriate choice of \(\theta\) i.e., replace \(\theta\) by \(-\theta\) in \(\mathbf{q}\) and you go from \(R_{\mathbf{q}}(\vec{v})\) to \(R_{\mathbf{q}^{\ast}}(\vec{v})\). In a nutshell, rotation perspective, personal preference, and even library conventions often decide the use of one operator over the other in a given application. It is important to note that both are mathematically equivalent and can represent the same rotations.

Quaternion Rotation Operator: Theorems

I present to you, without formal proof, the two theorems that summarise the two quaternion rotation operators \(R_{\mathbf{q}}(\vec{v})\) and \(R_{\mathbf{q}^{\ast}}(\vec{v})\).

Theorem 1: For any unit quaternion \(\mathbf{q} = q_0 + \vec{q} = \cos \theta + \vec{u} \sin \theta\) and for any vector \(\vec{v} \in \mathbb{R}^3\), the action of the operator \(R_{\mathbf{q}}(\vec{v}) = \mathbf{q} \star \vec{v} \star \mathbf{q}^{\ast}\) on \(\vec{v}\) may be interpreted geometrically as a rotation of the vector \(\vec{v}\) through an angle \(2\theta\) about \(\vec{q}\) or \(\vec{u}\) as the axis of rotation.

Theorem 2: For any unit quaternion \(\mathbf{q} = q_0 + \vec{q} = \cos \theta + \vec{u} \sin \theta\) and for any vector \(\vec{v} \in \mathbb{R}^3\), the action of the operator \(R_{\mathbf{q}^{\ast}}(\vec{v}) = \mathbf{q}^{\ast} \star \vec{v} \star \mathbf{q}\) on \(\vec{v}\) may be interpreted geometrically

  • as a rotation of the coordinate frame with respect to the vector \(\vec{v}\) through an angle \(2\theta\) about \(\vec{q}\) or \(\vec{u}\) as the axis, or,
  • an opposite rotation of the vector \(\vec{v}\) with respect to the coordinate frame through an angle \(2\theta\) about \(\vec{q}\) or \(\vec{u}\) as the axis.

While the conjectural proof above may be intuitive and perhaps sufficient for some readers, I refer the more curious to Chapter 15.15 of for the full formal proofs of Theorem 1 and 2.

Quaternion Operator Sequences

We often find ourselves applying a sequence of rotations to the robot in many applications. To that end, it helps to know that the quaternion operators elegantly handle rotation sequences.

Theorem 3: Suppose that \(\mathbf{p}\) and \(\mathbf{q}\) are unit quaternions which define the quaternion rotation operators \(R_{\mathbf{p}}(\vec{u}) = \mathbf{p} \star \vec{u} \star \mathbf{p}^{\ast}\) and \(R_{\mathbf{q}}(\vec{v}) = \mathbf{q} \star \vec{v} \star \mathbf{q}^{\ast}\). Then the quaternion product \(\mathbf{q} \star \mathbf{p}\) defines a quaternion rotation operator \(R_{\mathbf{q} \star \mathbf{p}}\) which represents a sequence of operators, \(R_{\mathbf{p}}\) followed by \(R_{\mathbf{q}}\). The axis and the angle of rotation are those represented by the quaternion product \(\mathbf{q} \star \mathbf{p}\).

The proof for which is easy and straightforward (for clarity, recall Complex Conjugate rules from ):

\[\begin{aligned} R_{\mathbf{q}}(R_{\mathbf{p}}(\vec{u})) &= R_{\mathbf{q}}(\mathbf{p} \star \vec{u} \star \mathbf{p}^{\ast}) \\ &= \mathbf{q} \star (\mathbf{p} \star \vec{u} \star \mathbf{p}^{\ast}) \star \mathbf{q}^{\ast} \\ &= (\mathbf{q} \star \mathbf{p}) \star \vec{u} \star (\mathbf{q} \star \mathbf{p})^{\ast} \\ &= R_{\mathbf{q} \star \mathbf{p}}(\vec{u}) \end{aligned}\]

Without much effort, one can easily extend Theorem 3 to the \(R_{\mathbf{q}^{\ast}}\) case.

Theorem 4: Suppose that \(\mathbf{p}\) and \(\mathbf{q}\) are unit quaternions which define the quaternion rotation operators \(R_{\mathbf{p}^{\ast}}(\vec{u}) = \mathbf{p}^{\ast} \star \vec{u} \star \mathbf{p}\) and \(R_{\mathbf{q}^{\ast}}(\vec{v}) = \mathbf{q}^{\ast} \star \vec{v} \star \mathbf{q}\). Then the quaternion product \(\mathbf{p} \star \mathbf{q}\) defines a quaternion rotation operator \(R_{(\mathbf{p} \star \mathbf{q})^{\ast}}\) which represents a sequence of operators, \(R_{\mathbf{p}^{\ast}}\) followed by \(R_{\mathbf{q}^{\ast}}\). The axis and the angle of rotation are those represented by the quaternion product \(\mathbf{p} \star \mathbf{q}\).

The proof for Theorem 4 follows the same line of argument as that of Theorem 3’s so I leave that to you. To that end, I refer the readers to Chapter 15.16 of for more discussion and examples on this.

Conclusion

This concludes my attempt to introduce robotics practitioners to quaternions and their rotation operators. Perhaps now is a good time to watch Grant Sanderson, a.k.a Mathematics YouTuber 3Blue1Brown’s videos on quaternions.

As we conclude this journey, I urge you to venture further into the realm of quaternions as a Riemannian manifold. Riemannian manifolds are mathematical spaces that, like quaternions, possess local and global geometrical properties. They extend our understanding of spaces beyond the familiar Euclidean world, allowing us to model curved surfaces. To that end, I want to emphasize that treating unit quaternions as a Riemannian manifold has huge implications for optimization, imitation learning and other robotics applications. Through numerous research works, it has been shown that the marriage of quaternions and Riemannian geometry enables us to tackle complex problems with newfound precision and insight.

May your explorations be filled with wonder and revelation.