Quaternions: Basic Algebra

A brief introduction to quaternions and their basic algebra

Citation Note: For this article, I have borrowed many things, sometimes “as is”, from:

  • Prof. Jack B. Kuipers’ seminal 1999 book
  • Prof. Hans-Peter Schröcker’s talk at IROS 2022
  • Prof. Andrew Hanson’s book on quaternions
  • Section I of Keith Conrad’s notes.

This article merely reproduces their work, perhaps put together concisely in one place. My motivation to write this is twofold - to provide robotics practitioners a one-stop-shop entry point to quaternions and challenge/improve my understanding of them. I claim no expertise in this topic but found it so fascinating that I decided to write about it.

Prerequisites: This is [1/3] article in my series on quaternions. For this article, I assume no familiarity with quaternions, to the point that some parts may come across as pedantic. I do not, however, talk about representing 3D rotations via quaternions in this one, I leave that to my next article. My goal here is only to ensure readers get comfortable with the idea of quaternion addition, multiplication, conjugate, and norm.

Motivation

Quaternions can efficiently represent rotations in 3D Euclidean space. Alternatively, one can turn to Euler angles or to \(3 \times 3\) orthogonal matrices with determinant \(1\) i.e., rotation matrices. While rotation matrices are great in their own right, for their nine elements, they have only three degrees of freedom (redundant information) and lack geometric interpretation in their natural formWell, determining rotation axis and angle need a few steps of calculations.. On the other hand, a quaternion is a 4-tuple that represents 3D rotations but with a more concise form with arguably better geometric interpretations. It elegantly sidesteps the Gimbal Lock and ambiguity problems of Euler angles and numerical error accumulation problems of rotation matrices. Quaternions also provide a natural way of interpolating between orientations.

To that end, I refer the readers to Chapter 2 of Prof. Andrew Hanson’s book “Visualizing Quaternions” where he rigorously discusses how both NASA astronauts and Hollywood film directors may prefer quaternions over other representations.

History

Quaternions were introduced by W. R. Hamilton in 1843. The complex number we learn in highschool is a sum \(a+ib\) with \(a, b \in \mathbb{R}\) and \(i^2 = -1\). Addition and multiplication rules are given by

\[\begin{aligned} (a + ib) + (c + id) & = (a + b) + (b + d)i \\ (a + ib)(c + id) & = (ac - bd) + (ad + bc)i \end{aligned}\]

Hamilton avoided explaining what \(i\) is by declaring \(a+ib\) as ordered pairs \((a,b) \in \mathbb{R}^2\) with the following rules

\[\begin{aligned} (a, b) + (c, d) & = (a + c, b + d) \\ (a, b)(c, d) & = (ac - bd)(ad + bc) \\ (a, b) + (0, 0) & = (a, b) \quad \text{(Additive identity)} \\ (a, b)(1, 0) & = (a, b) \quad \text{(Multiplicative identity)} \end{aligned}\]

So \((a,b) = (a,0) + (0,b) = a(1,0) + b(0,1)\) is essentially \(a+ib\) if we define \(i\) as \((0, 1)\). While trying to extend this to three dimensions and find triples \((a, b, c)\), he instead discovered a way to multiply in four dimensions at the cost of abandoning commutativity of multiplcation. Legend has it that the idea to add the fourth dimension struck him while walking with his wife Helen at the Royal Irish Academy, and that he noted down the quaternion equations as they passed the Broom Bridge of the Royal Canal. A stone plaque at the exact location carved with the following equations was later commemorated:

\[i^2 = j^2 = k^2 = ijk = -1\]
Source: Wikipedia

If mathematics and its history interests you, I refer you to this YouTube video by “Kathy Loves Physics and History”. In a subsequent video, she explains how the discovery of quaternions (with Maxwell’s equations) ultimately led to Vector Analysis.

Definition

The quaternions are

\[\mathbb{H} = \{a + bi + cj + dk: a, b, c, d \in \mathbb{R}\},\]

where the following rules are imposed:

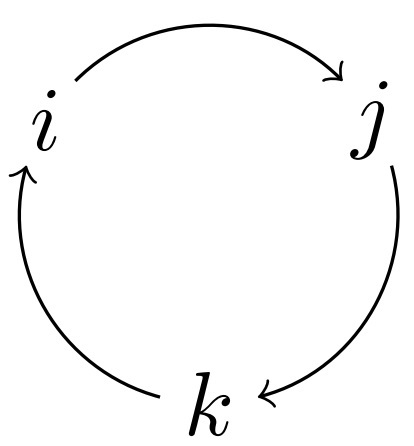
One could always look at the circle below to remember the multiplicative rules of \(i, j, k\). Products following the below order get a plus sign, otherwise a minus sign, \(e.g., ij = k\) and \(ji = -k\).

Source: Keith Conrad

Quick Comparison with Complex Numbers

Complex Numbers \(\mathbb{C}\) \(c = a +bi, \quad a,b \in \mathbb{R}, \quad i^2=-1\)
Complex Conjugate \(c^{\ast} = a -bi\)
Real Part \(\text{Re}(c) = \frac{1}{2}(c + c^{\ast}) = a\)
Imaginary Part \(\text{Im}(c) = \frac{1}{2}(c - c^{\ast}) = b\)
Quadrance and Norm \(cc^{\ast} = a^2 + b^2, \quad \Vert c \Vert = \sqrt{cc^{\ast}}\)
Inverse \(c^{-1} = \frac{c^{\ast}}{cc^{\ast}}\)

Even though we haven’t seen how two quaternions add and multiply in detail, the following table summarizes most of theis article in a concise way.

Quaternions \(\mathbb{H}\) \(\mathbf{q} = q_0 + q_1i + q_2j + q_3k, \ q_n \in \mathbb{R}, \ i^2 = j^2 = k^2 = ijk = -1\)
Complex Conjugate \(\mathbf{q}^{\ast} = q_0 - q_1i - q_2j - q_3k\)
Real Part \(\text{Re}(\mathbf{q}) = \frac{1}{2}(\mathbf{q} + \mathbf{q}^{\ast}) = q_0\)
Imaginary Part \(\text{Im}(\mathbf{q}) = \frac{1}{2}(\mathbf{q} - \mathbf{q}^{\ast}) = q_1i +q_2j + q_3k\)
Quadrance and Norm \(\mathbf{q}\mathbf{q}^{\ast} = q_0^2 + q_1^2 + q_3^2 + q_4^2, \quad \Vert \mathbf{q} \Vert = \sqrt{\mathbf{q}\mathbf{q}^{\ast}}\)
Inverse \(\mathbf{q}^{-1} = \frac{\mathbf{q}^{\ast}}{\mathbf{q}\mathbf{q}^{\ast}}\)

An Example for Clarity

Solve \((3i - 5j)(5k + 9i)\).

\[\begin{aligned} & \Rightarrow 3i \times 5k + 3i \times 9i - 5j \times 5k - 5j \times 9i \\ & \Rightarrow 15(ik) + 27(i^2) - 25(jk) - 45(ji) \\ & \Rightarrow 15(-j) + 27(-1) - 25(i) - 45(-k) \\ & \Rightarrow -27 -25i -15j + 45k \end{aligned}\]

Quaternion Models

There is more than one way to interpret quaternions. Some are more intuitive than others and we see three below.

Four-Dimensional Vectors

A straightforward way of thinking about quaternions is to treat them as four-dimensional vectors.

\[\begin{aligned} \mathbf{p} & = p_0 + p_1i + p_2j + p_3k = (p_0, p_1, p_2, p_3)^{\top} \\ \mathbf{q} & = q_0 + q_1i + q_2j + q_3k = (q_0, q_1, q_2, q_3)^{\top} \end{aligned}\]

To avoid operator overload with the dot product, I introduce \(\star\) as the quaternion multiplication operator. Now, the quaternion multiplication between \(\mathbf{p}\) and \(\mathbf{q}\) can be written in matrix form as follows See the following subsection for a full derivation of quaternion multiplication.

\[\begin{aligned} \mathbf{p} \star \mathbf{q} &= \left[ \begin{matrix} p_0q_0 - p_1q_1 - p_2q_2 - p_3q_3 \\ p_0q_1 + p_1q_0 + p_2q_3 - p_3q_2 \\ p_0q_2 - p_1q_3 + p_2q_0 + p_3q_1 \\ p_0q_3 + p_1q_2 - p_2q_1 + p_3q_0 \end{matrix} \right] \\ &= \left[ \begin{matrix}p_0 & -p_1 & -p_2 & -p_3 \\ p_1 & p_0 & -p_3 & -p_2 \\ p_2 & p_3 & p_0 & -p_1 \\ p_3 & -p_2 & p_1 & p_0\end{matrix} \right] \left[ \begin{matrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{matrix} \right] = \mathbf{P}. \mathbf{q} \end{aligned}\]

It can be convenient to represent quaternion multiplication using matrix multiplication. One can see that \(\mathbf{P}\) is an orthogonal matrix (\(\mathbf{P}^{\top} \mathbf{P} = I_4\)) in 4D Euclidean space. However, this model still lacks geometric interpretations in 3D.

Two-By-Two Matrices

Another way of thinking about quaternions is to treat them as products of simple \(2 \times 2\) matrices:

\[\begin{aligned} U &:= \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\right], \; I := \left[ \begin{matrix} i & 0 \\ 0 & -i \end{matrix}\right], \\ J &:= \left[ \begin{matrix} 0 & 1 \\ -1 & 0 \end{matrix}\right], \; K := \left[ \begin{matrix} 0 & i \\ i & 0 \end{matrix}\right] \end{aligned}\] \[I^2 = J^2 = K^2 = IJK = -U\]

Then we have

\[\begin{aligned} \mathbf{q} & \approx Q = q_0U + q_1I + q_2J + q_3K \\ \mathbf{q^{\ast}} & \approx adj(Q), \quad \mathbf{qq^{\ast}} \approx det(Q) \quad \mathbf{q}^{-1} \approx Q^{-1} \end{aligned}\]

As Prof. Schröcker says in his presentation - “When in doubt, think of matrix multiplication!”.

Scalar + Vector

This is perhaps the most interesting model and from now on, we stick to this one. Recall from the comparisons with complex numbers, we define the real and imaginary parts of a quaternion as follows:

\[\begin{aligned} \text{Re}(\mathbf{q}) & = \frac{1}{2}(\mathbf{q} + \mathbf{q}^{\ast}) = q_0 \quad \text{(Scalar Part)} \\ \text{Im}(\mathbf{q}) & = \frac{1}{2}(\mathbf{q} - \mathbf{q}^{\ast}) = q_1i +q_2j + q_3k \quad \text{(Vector Part)} \end{aligned}\]

Assuming the standard orthonormal basis for \(\mathbb{R}^3\) is given by three unit vectors \(i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1)\), quaternions can be seen as a sum of a \(q_0\) scalar and a vector \(\vec{q} = (q_1, q_2, q_3)\). Namely,

\[\mathbf{q} = q_0 + q_1i + q_2j + q_3k = q_0 + \vec{q}\]

Which makes \(\mathbb{H} = \mathbb{R} \oplus \mathbb{R}^3\). This has major geometric significance and you will soon see why. With this, it should be straightforward to derive addition and multiplication equations for two quaternions now.

Quaternion Algebra

Let us derive the basic quaternion operations in Scalar + Vector form.

Addition

Addition operation is rather straightforward from our understanding of scalar and vector additions.

\[\begin{aligned} \mathbf{p} + \mathbf{q} & = (p_0 + q_0) + (p_1 + q_1)i + (p_2 + q_2)j + (p_3 + q_3)k \\ & = (p_0 + q_0) + (\vec{p} + \vec{q}) \end{aligned}\]

Multiplication

Similar to addition, first, let us write out the multiplication of two quaternions the naive way and see if we can transform it to the Scalar + Vector form.

\[\begin{aligned} \mathbf{p} \star \mathbf{q} &= (p_0 + p_1i + p_2j + p_3k) (q_0 + q_1i + q_2j + q_3k) \\ \\ &= p_0q_0 + p_0(q_1i + q_2j + q_3k) + p_1q_0i \\ &\quad + p_1i(q_1i + q_2j + q_3k) + p_2q_0j + p_2j(q_1i + q_2j + q_3k) \\ &\quad + p_3q_0k + p_3k(q_1i + q_2j + q_3k) \\ \\ &= p_0q_0 + p_0(q_1i + q_2j + q_3k) + p_1q_0i + p_1q_1(i^2) \\ &\quad + p_1q_2(ij) + p1q_3(ik) + p_2q_0j + p_2q_1(ji) \\ &\quad + p_2q_2(j^2) + p_2q_3(jk) + p_3q_0k + p_3q_1(ki) \\ &\quad + p_3q_2(kj) + p_3q_3(k^2) \\ \\ & = p_0q_0 + p_0(q_1i + q_2j + q_3k) + q_0(p_1i + p_2j+ p_3k) + p_1q_1(i^2) \\ &\quad + p_1q_2(ij) + p_1q_3(ik) + p_2q_1(ji) + p_2q_2(j^2) \\ &\quad + p_2q_3(jk) + p_3q_1(ki) + p_3q_2(kj) + p_3q_3(k^2) \\ \\ &= p_0q_0 + p_0(q_1i + q_2j + q_3k) + q_0(p_1i + p_2j+ p_3k) + p_1q_1(-1) \\ &\quad + p_1q_2(k) + p_1q_3(-j) + p_2q_1(-k) + p_2q_2(-1) \\ &\quad + p_2q_3(i) + p_3q_1(j) + p_3q_2(-i) + p_3q_3(-1) \\ \\ &= p_0q_0 + p_0\textcolor{orange}{(q_1i + q_2j + q_3k)} + q_0\textcolor{lime}{(p_1i + p_2j+ p_3k)} \\ &\quad - \textcolor{cyan}{(p_1q_1+p_2q_2 +p_3q_3)} \\ &\quad + \textcolor{pink}{(p_2q_3 - p_3q_2)i + (p_3q_1 - p_1q_3)j} + \textcolor{pink}{(p_1q_2 - p_2q_1)k} \hspace{5cm} \end{aligned}\]

Phew! Reminiscent of the Four-Dimensions model, one can see how quickly quaternion products in their naive form become cumbersome, unintuitive and inconvenient. Thankfully, the Scalar + Vector model allows us to rewrite the above equation in terms of dot and cross products as follows:

\[\mathbf{p} \star \mathbf{q} = p_0q_0 -\textcolor{cyan}{\vec{p} \cdot \vec{q}} + p_0\textcolor{orange}{\vec{q}} + q_0\textcolor{lime}{\vec{p}} + \textcolor{pink}{\vec{p} \times \vec{q}} \tag{1}\]

This is great! Finally, we reach a point where we can simply add scalars (\(p_0q_0 -\textcolor{cyan}{\vec{p} \cdot \vec{q}}\)) and 3D vectors (\(p_0\textcolor{orange}{\vec{q}} + q_0\textcolor{lime}{\vec{p}} + \textcolor{pink}{\vec{p} \times \vec{q}}\)) to compute quaternion multiplication. Eq. \(\text{(1)}\) allows us to make the following observations:

Complex Conjugate

The conjugate of a quaternion \(\mathbf{q}\) is denoted by \(\mathbf{q^{\ast}}\) and defined as

\[\mathbf{q^{\ast}} = q_0 - q_1i - q_2j - q_3k = q_0 - \vec{q} \tag{2}\]

From the definition, it follows that:

\[\begin{aligned} (\mathbf{q^{\ast}})^{\ast} & = q_0 - (-\vec{q}) = \mathbf{q} \\ \mathbf{q} + \mathbf{q^{\ast}} & = 2q_0 \\ \mathbf{q} - \mathbf{q^{\ast}} & = 2\vec{q} \\ \mathbf{q^{\ast}} \star \mathbf{q} & = (q_0 - \vec{q}) \star (q_0 + \vec{q}) \\ & = q_0q_0 - (-\vec{q}) \cdot \vec{q} + q_0\vec{q} \\ & \quad + (-\vec{q})q_0 + (-\vec{q}) \times \vec{q} \quad \text{(from Eq. (1))} \\ & = q_0^2 + \vec{q} \cdot \vec{q} \\ & = q_0^2 + q_1^2 + q_2^2 + q_3^2 \quad \text{(Quadrance)} \\ & = \mathbf{q} \star \mathbf{q^{\ast}} \quad \text{(Commutative)} \\ \end{aligned}\]

We can also easily derive the conjugate of a quaternion multiplication.

\[\begin{aligned} (\mathbf{p} \star \mathbf{q})^{\ast} & = (p_0q_0 -\vec{p} \cdot \vec{q} + p_0\vec{q} + q_0\vec{p} + \vec{p} \times \vec{q})^{\ast} \quad \text{(from Eq. (1))}\\ & = (p_0q_0 -\vec{p} \cdot \vec{q} - p_0\vec{q} - q_0\vec{p} - \vec{p} \times \vec{q}) \quad \text{(from Eq. (2))}\\ & = (p_0q_0 -(-\vec{p}) \cdot (-\vec{q}) + p_0(-\vec{q}) \\ & \quad + q_0(-\vec{p}) - (-\vec{p}) \times (-\vec{q})) \quad \text{(Since } a \times b = (-a \times -b)\text{)}\\ & = (p_0q_0 -(-\vec{p}) \cdot (-\vec{q}) + p_0(-\vec{q}) \\ & \quad + q_0(-\vec{p}) + (-\vec{q}) \times (-\vec{p})) \quad \text{(Since } a \times b = - (b \times a)\text{)}\\ & = \mathbf{q}^{\ast} \star \mathbf{p}^{\ast} \hspace{10cm} \text{(3)} \end{aligned}\]

With Eq. \(\text{(3)}\), we can now easily find the conjugate of quaternion multiplications of more than two quaternions and you see that the above form extends. Given four quaternions \(\mathbf{q}_1, \mathbf{q}_2, \mathbf{q}_3\) and \(\mathbf{q}_4\), we have

\[\begin{aligned} (\mathbf{q}_1 \star \mathbf{q}_2 \star \mathbf{q}_3)^{\ast} &= ((\mathbf{q}_1 \star \mathbf{q}_2) \star \mathbf{q}_3)^{\ast}\\ &= \mathbf{q}_3^{\ast} \star (\mathbf{q}_1 \star \mathbf{q}_2)^{\ast} \quad \text{(from Eq. (3))}\\ &= \mathbf{q}_3^{\ast} \star \mathbf{q}_2^{\ast} \star \mathbf{q}_1^{\ast} \\ (\mathbf{q}_1 \star \mathbf{q}_2 \star \mathbf{q}_3 \star \mathbf{q}_4)^{\ast} &= ((\mathbf{q}_1 \star \mathbf{q}_2) \star (\mathbf{q}_3 \star \mathbf{q}_4))^{\ast} \\ &= (\mathbf{q}_3 \star \mathbf{q}_4)^{\ast} \star (\mathbf{q}_1 \star \mathbf{q}_2) ^{\ast} \\ &= \mathbf{q}_4^{\ast} \star \mathbf{q}_3^{\ast} \star \mathbf{q}_2^{\ast} \star \mathbf{q}_1^{\ast} \\ \end{aligned}\]

Norm

The squared norm of a quaternion \(\mathbf{q}\) is simply its quadrance

\[\begin{aligned} \Vert \mathbf{q} \Vert^2 &= q_0^2 + q_1^2 + q_2^2 + q_3^2 \\ &= \mathbf{q^{\ast}} \star \mathbf{q} = \mathbf{q} \star \mathbf{q^{\ast}} \\ &= q_0^2 + (\vec{q} \cdot \vec{q}) \end{aligned}\]

Deriving an equation for the squared norm of the quaternion product is easier with quadrance.

\[\begin{aligned} \Vert \mathbf{p} \star \mathbf{q} \Vert^2 &= (\mathbf{p} \star \mathbf{q}) \star (\mathbf{p} \star \mathbf{q})^{\ast} \\ &= \mathbf{p} \star \mathbf{q} \star \mathbf{q}^{\ast} \star \mathbf{p}^{\ast} \quad \text{(from Eq. (3))}\\ &= \mathbf{p} \star \Vert \mathbf{q} \Vert^2 \star \mathbf{p}^{\ast} \\ &= \Vert \mathbf{q} \Vert^2 \mathbf{p} \star \mathbf{p}^{\ast} \quad \text{(Scalars commute with quaternions)} \\ &= \Vert \mathbf{q} \Vert^2 \Vert \mathbf{p} \Vert^2 \hspace{12cm} \text{(4)}\\ \end{aligned}\]

This relationship extends to higher-order quaternion multiplication as well. Given \(n\) quaternions \(\{\mathbf{q}_1, \mathbf{q}_2, ... \mathbf{q}_n\}\), one could easily derive the following

\[\begin{aligned} \Vert \mathbf{q}_1 \star \mathbf{q}_2 \star \mathbf{q}_3 \Vert^2 &= \Vert \mathbf{q}_1 \Vert^2 \Vert \mathbf{q}_2 \Vert^2 \Vert \mathbf{q}_3 \Vert^2 \\ \Vert \mathbf{q}_1 \star \mathbf{q}_2 \star \mathbf{q}_3 \star \mathbf{q}_4 \Vert^2 &= \Vert \mathbf{q}_1 \Vert^2 \Vert \mathbf{q}_2 \Vert^2 \Vert \mathbf{q}_3 \Vert^2 \Vert \mathbf{q}_4 \Vert^2 \\ \Vert \mathbf{q}_1 \star ... \star \mathbf{q}_n \Vert^2 &= \Vert \mathbf{q}_1 \Vert^2 ... \Vert \mathbf{q}_n \Vert^2 \hspace{8.5cm} \text{(5)} \end{aligned}\]

Inverse

The inverse of a quaternion \(\mathbf{q}\) is defined as

\[\mathbf{q}^{-1} = \frac{\mathbf{q^{\ast}}}{\mathbf{q^{\ast}} \star \mathbf{q}} \quad \Rightarrow \mathbf{q}^{-1} \star \mathbf{q} = 1\]

Conclusion

In this article, we’ve delved into the seemingly peculiar realm of quaternion algebra. We started by introducing quaternions as a four-dimensional extension of complex numbers, consisting of a real part and three imaginary components. We looked into some commonly used quaternion models, and then explored the Scalar + Vector model’s arithmetic operations and properties, including addition, scalar and quaternion multiplication, complex conjugate, norm and inverse and discussed the source of non-commutativity of their multiplication. In my next article , we’ll take this understanding a step further by exploring how quaternions can be easily extended to form a rotation operator in \(\mathbb{R}^3\).